En análisis numérico, la regla o método de Simpson (nombrada así en honor de Thomas Simpson) es un método de integración numérica que se utiliza para obtener la aproximación de la integral:
![\int_{a}^{b} f(x) \, dx \approx \frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right]](http://upload.wikimedia.org/math/8/0/c/80ca47af148fedc25f9b42d84725c0b2.png) .
.
Derivación de la regla de Simpson
Consideramos el polinomio interpolante de orden dos P2(x), que aproxima a la función integrando f(x) entre los nodos x0 = a, x1 = b y m = (a+b)/2. La expresión de ese polinomio interpolante, expresado a través de la Interpolación polinómica de Lagrange es:
Así, la integral buscada se puede aproximar como:
Error
El error al aproximar la integral mediante la Regla de Simpson es
donde h = (b − a) / 2 y ![\xi \in [a, b]](http://upload.wikimedia.org/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) .
.
Regla de Simpson compuesta
En el caso de que el intervalo [a,b] no sea lo suficientemente pequeño, el error al calcular la integral puede ser muy grande. Para ello, se recurre a la fórmula compuesta del trapecio. Dividiremos el intervalo [a,b] en n subintervalos iguales, de manera que xi = a + ih, donde h = (b −a) / n para i = 0,1,...,n.
Aplicando la Regla de Simpson a cada subintervalo, tenemos:
Sumando las integrales de todos los subintervalos, llegamos a que:
El máximo error viene dado por la expresión 
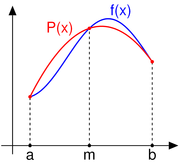

![\int_{a}^{b} f(x) \, dx\approx \int_{a}^{b} P_2(x) \, dx =\frac{h}{3}\left[f(a) + 4f(m)+f(b)\right].](http://upload.wikimedia.org/math/1/8/e/18ea318129761a9f35647679f09906b6.png)

![\int_{x_{j-1}}^{x_j} f(x)\, dx = \frac{x_{j}-x_{j-1}}{6}\left[f(x_{j-1}) + 4f\left(\frac{x_{j-1}+x_j}{2}\right)+f(x_j)\right] j=1, ..., n.](http://upload.wikimedia.org/math/3/d/1/3d10ce8cc801220d10219d2939f60ea6.png)
![\int_a^b f(x) \, dx\approx \frac{h}{3}\bigg[f(x_0)+2\sum_{j=1}^{n/2-1}f(x_{2j})+ 4\sum_{j=1}^{n/2}f(x_{2j-1})+f(x_n) \bigg],](http://upload.wikimedia.org/math/a/c/2/ac281e21c702c7a01b4270ada92baa27.png)
No hay comentarios:
Publicar un comentario