lunes, 1 de diciembre de 2008

INVERSION DE MATRICES

En matemáticas, y especialmente en álgebra lineal, una matriz cuadrada A de orden n se dice que es invertible, no singular, no degeneradao regular si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A−1, tal que

AA−1 = A−1A = In,

donde In es la matriz identidad de orden n y el producto utilizado es el producto de matrices usual.

Una matriz no invertible se dice que es singular o degenerada. Una matriz es singular si y solo si su determinante es cero.

La inversión de matrices es el proceso de encontrar la matriz inversa de una matriz dada.


Propiedades de la matriz inversa 

]

  • La inversa de una matriz, si existe, es única.
  • La inversa del producto de dos matrices es el producto de las inversas cambiando el orden:
\left (B \cdot A \right ) ^{-1} = {A}^{-1} \cdot {B}^{-1}
  • Si la matriz es invertible, también lo es su traspuesta, y el inverso de su traspuesta es la transpuesta de su inversa, es decir:
\left(A^{T}\right)^{-1} = \left(A^{-1}\right)^{T}
  • Y, evidentemente:
\left(A^{-1}\right)^{-1} = A
  • Una matriz es invertible si y sólo si el determinante de A es distinto de cero. Además la inversa satisface la igualdad:
{A^{-1}} = {1 \over {\begin{vmatrix} A \end{vmatrix}}} \ (adj(A^{T})) \

donde  { {\begin{vmatrix} A \end{vmatrix}}} es el determinante de A y  \ adj{(A^{T})} \  es la matriz de adjuntos de la traspuesta de A.

Demostración de la unicidad de la inversa 

Supongamos que B y C son inversas de A

AB = BA = I

AC = CA = I

Multiplicando por C

(BA)C = IC = C

(BA)C = B(AC) = BI = B

De modo que B=C y se prueba que la inversa es única.

Demostración del criterio de inversibilidad de las matrices cuadradas 

Se probará la doble implicación.

Necesidad (\Rightarrow) 

Suponiendo que existe B tal que AB = BA = I. Entonces al aplicar la función determinante se obtiene

\det\left(AB\right)=\det\left(BA\right)=\det\left(I\right)

usando la propiedad det(I) = 1

\det\left(A\right)\det\left(B\right)=1

Por lo tanto, det(A) es distinto de cero.

\det\left(A\right)\neq0

Suficiencia (\Leftarrow) 

Suponiendo que el determinate de A es distinto de cero, sea aij es el elemento ij de la matriz A y sea Aij la matriz A sin la fila i y la columna j(comúnmente conocida como j-ésimo menor de A). Entonces

\det(A)= \sum_{i=1}^n (-1)^{i+j}a_{ij}\det(A_{ij})

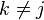Sea k\neq j, entonces

\sum_{i=1}^n (-1)^{i+j}a_{ik}\det(A_{ij})=0

Esta afirmación es válida propiedades de los determinantes, pues la parte izquierda de la relación nos conduce a una matriz con la columna jigual a la columna k y los demás términos iguales a los de A. Entonces

\delta_{jk}\det\left(A\right)= \sum_{i=1}^n (-1)^{i+j}\det\left(A_{ij}\right)a_{ik}

donde δjk = 1 cuando j = k y δjk = 0 cuando 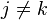j\neq k. Entonces

\det\left(A\right)I = \left(\mbox{adj}(A)\right)^tA

Es decir que A tiene inversa izquierda

\frac{\left(\text{adj}(A)\right)^t}{\det\left(A\right)}

Como \left(\text{adj}(A)\right)^t = \text{adj}\left(A^t\right), entonces At también tiene inversa izquierda que es

\frac{\left(\text{adj}(A^t)\right)^t}{\det\left(A^t\right)}= \frac{\text{adj}(A)}{\det\left(A\right)}

Entonces

\frac{\text{adj}(A)}{\det\left(A\right)}A^t=I

luego, aplicando la transpuesta

A\frac{\left(\text{adj}(A)\right)^t}{\det\left(A\right)}=I

Que es lo que se quería demostrar

Métodos de inversión de matrices 

Solución analítica 

Inversión de matrices 2×2 

Calcular la matriz inversa en matrices de 2x2 puede ser muy sencillo. Se puede hacer de la siguiente manera: 1

\mathbf{A}^{-1} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}^{-1} = \frac{1}{ad - bc} \begin{bmatrix} \,\,\,d & \!\!-b \\ -c & \,a \\ \end{bmatrix}.

Esto es posible siempre y cuando ad - bc, el determinante de la matriz, no sea cero.

Inversión de matrices de órdenes superiores 

Para matrices de ordenes superiores puede utilizarse la siguiente fórmula:

{A^{-1}} = {1 \over {\begin{vmatrix} A \end{vmatrix}}} \ (adj(A)) \

donde  { {\begin{vmatrix} A \end{vmatrix}}} es el determinante de A y  \ adj{(A)} \  es la matriz de adjuntos de A.

Métodos numéricos 

El método de eliminación de Gauss-Jordan puede utilizarse para determinar si una determinada matriz es invertible y para encontrar su inversa. Una alternativa es la descomposición LU, que descompone una matriz dada como producto de dos matrices triangulares, una inferior y otra superior, mucho más fáciles de invertir.
Publicado por en

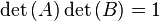
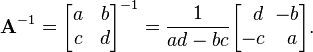
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)