matenumerica RUIZ RUEDA LUIS: CALCULO DE DETERMINANTES

Cauchy fue el primero en emplear el término determinante con su significado moderno. Se encargó de realizar una síntesis de los conocimientos anteriores y publicó en 1812 la fórmula del determinante de un producto. Ese mismo año Binet ofreció una demostración para dicha fórmula. Paralelamente Cauchy establece las bases del estudio de la reducción de endomorfismos.

Con la publicación de sus tres tratados sobre determinantes en 1841 en la revista Crelle, Jacobi aporta a la noción una gran notoriedad. Por primera vez presenta métodos sistemáticos de cálculo bajo una forma algorítmica. Del mismo modo, hace posible la evaluación del determinante de funciones con instauración del jacobiano.

El cuadro matricial es introducido por los trabajos de Cayley y James Joseph Sylvester. Un determinante de orden 3 se calcula mediante laregla de Sarrus:

Determinantes de orden superior a 3

Suelen desarrollarse el determinante de orden n a partir de una fila o columna, eliminando así filas y columnas hasta obtener un determinante de orden n-1. Para ello se toma una fila o columna cualquiera, multiplicando cada elemento por su adjunto (es decir, el determinante de la matriz que se obtiene eliminando la fila y columna correspondiente a dicho elemento, multiplicado por (-1)^i+j donde i es el numero de fila y j el numero de columna. Para el primer elemento, se eleva al cuadrado, por lo que (-1)² = 1. El segundo se eleva al cubo, (-1)³ = -1. Se observa que los signos iran alternando de un elemento al siguiente). Luego, se suman todos los productos, y se obtiene el determinante. En caso de un determinante de orden 4, se obtienen directamente determinantes de orden 3 que podrán ser calculados por la regla de Sarrus. En cambio, en los determinantes de orden superior, como por ejemplo n = 5, al desarrollar los elementos de una línea, obtendremos determinantes de orden 4, que a su vez se deberán desarrollar en por el mismo método, para obtener determinantes de orden 3.

La cantidad de operaciones aumenta muy rápidamente. En el peor de los casos (sin obtener ceros en filas y columnas), para un determinante de orden 4 se deberán desarrollar 4 determinates de orden 3. En un determinante de orden 5, se obtienen 5 determinates de orden 4 a desarrollar, dándonos 20 determinates de orden 3. El numero de determinates de orden 3 que se obtienen en el desarrollo de un determinante de orden n es igual a 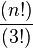$(n!) \over (3!)$

Por ejemplo, mediante este método, para un determinante de orden 10 se deberán calcular 10 x 9 x 8 x 7 x 6 x 5 x 4 = ¡604.800 determinantes de orden 3!.

También se pueden aplicar operaciones elementales entre filas y columnas para lograr la mayor cantidad de ceros en una fila o columna, conocido como metodo de Gauss. De esta manera se reduce notablemente la cantidad de calculos. Por ejemplo, para obtener con el método especificado un determinante de orden 4, se deben calcular 4 determinantes de orden 3. En cambio, si previamente se logran tres ceros en una fila o columna, bastara con calcular solo un determinante de orden 3 (ya que los demas determinantes estarán multiplicados por 0, lo que los anula). También puede utilizarse el Método de eliminación Gaussiana, para convertir la matriz en una matriz triangular. Si bien el proceso puede parecer tedioso, estará muy lejos de los 14.529.715.200 de determinantes de orden 3 necesarios para calcular el determinante de una matriz de orden 14.

Es también conveniente antes de realizar cualquiera de esas operaciones, observar atentamente el determinante y verificar que no existen casos especiales, como una combinación lineal, de lo que se deduciría al instante que el determinante es cero, o en el caso de una matriz triangular, donde el determinante es igual al producto de los elementos de la diagonal principal.

En general, sin embargo, los cálculos de determinantes de ordenes altos pueden realizarse mediante la programación de estos algoritmos enordenadores que realizan esos cálculos muy rápidamente.

Primeros ejemplos: áreas y volúmenes

El cálculo de áreas y volúmenes bajo forma de determinantes en espacios euclídeos aparecen como casos particulares de una noción más general de determinante. La letra mayúscula D (Det) se reserva a veces para distinguirlos.

Determinante de dos vectores en el plano euclídeo

Fig. 1. El determinante es el área azul orientada

Sea P el plano euclídeo. El determinante de los vectores X y X' se obtiene con la expresión analítica

$\det(X,X')=\begin{vmatrix} x & x' \\ y & y'\end{vmatrix}=xy'-yx'$

o, de manera equivalente, por la expresión geométrica

$\det(X,X')=\|X\|\cdot\|X'\|\cdot\sin \theta$

en la cual $θ$ es el ángulo orientado formado por los vectores X y X'.

Propiedades

El valor absoluto del determinante es igual a la superficie del paralelogramodefinido por X y X' ( $X sinθ$ es en efecto la altura del paralelogramo, por lo que A = Base × Altura).
El determinante es nulo si y sólo si los dos vectores son colineares (el paralelogramo se convierte en una línea).
Su signo es estrictamente positivo si y sólo si la medida del ángulo (X, X ') se encuentra en ]0, $π$ [.
La aplicación del determinante es bilineal: la linearidad respecto al primer vector se escribe

$\det(aX+bY,X')=a\det(X,X')+b\det(Y,X')\;$

y respecto al segundo

$\det(X,aX'+bY')=a\det(X,X')+b\det(X,Y')\;$

Fig. 2.Suma de las áreas de dos paralelogramos adyacentes.

La figura 2, en el plano, ilustra un caso particular de esta fórmula. Representa dos paralelogramos adyacentes, uno definido por los vectores u y v (en verde), y otro por los vectores u' y v (en azul). Es fácil ver sobre este ejemplo el área del paralelogramo definido por los vectores u+u' y v (en gris): es igual a la suma de los dos paralelogramos precedentes a la cual se sustrae el área de un triángulo y se añade el área de otro triángulo. Ambos triángulos se corresponden por translación y la fórmula siguiente se verifica Det(u+u', v)=Det(u, v)+Det(u', v).

El dibujo corresponde a un caso particular de la fórmula de bilinealidad ya que las orientaciones han sido elegidas de manera que las áreas tengan el mismo signo, aunque ayuda a comprender el contenido geométrico.

Generalización [editar]

Es posible definir la noción de determinante en un plano euclídeo orientado con una base ortonormal directa B utilizando las coordenadas de los vectores en esta base. El cálculo del determinante da el mismo resultado sea cual sea la base ortonormal directa elegida para el cálculo.

Determinante de tres vectores en el espacio euclídeo [editar]

Sea E el espacio euclídeo orientado de dimensión 3. El determinante de tres vectores de E se da por

$\det(X,X ',X '')=\begin{vmatrix} x & x' &x''\\ y & y'&y''\\ z&z'&z'' \end{vmatrix}=x \begin{vmatrix} y' & y'' \\ z' & z''\end{vmatrix} - x' \begin{vmatrix} y & y'' \\ z & z''\end{vmatrix} + x'' \begin{vmatrix} y & y' \\ z & z'\end{vmatrix} = xy'z''+x'y''z+x''yz'-xy''z'-x'yz''-x''y'z.$

Fig. 3. Ilustración gráfica de la trilinealidad

Este determinante lleva el nombre de producto mixto.

Propiedades [editar]

El valor absoluto del determinante es igual al volumen de paralelepípedo definido por los tres vectores.
El determinante es nulo si y sólo si los tres vectores se encuentran en un mismo plano (paralelepípedo "plano").
La aplicación determinante es trilineal: sobre todo

$\det(aX+bY,X ',X '')=a\det(X,X ',X '')+b\det(Y,X ',X '')\,$

Una ilustración geométrica de esta propiedad se da en la figura 3 con dos paralelepípedos adyacentes, es decir con una cara común. La igualdad siguiente es entonces intuitiva:

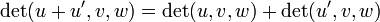$\det(u+u', v,w)=\det(u, v,w)+\det(u', v,w)\,$ .

Propiedades

El determinante de una matriz es un invariante algebraico, lo cual implica que dada una aplicación lineal todas las matrices que la represente tendrán el mismo determinante. Eso permite definir el valor del determinante no sólo para matrices sino también para apliaciones lineales.
Una propiedad fundamental del determinante es su comportamiento multiplicativo frente al producto de matrices:

$\det(\mathbf{AB}) = \det(\mathbf{A})\cdot\det(\mathbf{B})$

Eso implica en términos de aplicaciones lineales dada la relación existente entre la composición de aplicaciones lineales y el producto de matrices que las representan que, dadas dos aplicaciones linales 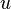$u\,$ y $v\,$ se tiene la siguiente igualdad:

$\det(u\circ v) = \det(u)\cdot\det(v)$

El determinante de una matriz y el de su traspuesta coinciden: $\det(A^t)=\det(A)\,$

Una aplicación lineal entre espacios vectoriales es invertible si y sólo si su determinante no es nulo. Por lo tanto, una matriz con coeficientes en un cuerpo es invertible si y sólo si su determinante es no nulo.

Matrices en bloques [editar]

Sean $A, B, C, D$ matrices $n\times n, n\times m, m\times n, m\times m$ respectivamente. Entonces

$\det\begin{pmatrix}A& 0\\ C& D\end{pmatrix} = \det\begin{pmatrix}A& B\\ 0& D\end{pmatrix} = \det(A) \det(D) .$ Esto se puede ver de la formula de Leibiniz Leibniz formula. Empleando la siguiente identidad

$\begin{pmatrix}A& B\\ C& D\end{pmatrix} = \begin{pmatrix}A& 0\\ C& I\end{pmatrix} \begin{pmatrix}I& A^{-1} B\\ 0& D - C A^{-1} B\end{pmatrix}$

vemos que para una matriz general

$\det\begin{pmatrix}A& B\\ C& D\end{pmatrix} = \det(A) \det(D - C A^{-1} B) .$

Analogamente, se puede obtener una identidad similar con $det(D)$ factorizado.⁶

Si $d i j$ son matrices diagonales,

$\det\begin{pmatrix}d_{11} & \ldots & d_{1c}\\ \vdots & & \vdots\\ d_{r1} & \ldots & d_{rc} \end{pmatrix} = \det \begin{pmatrix}\det(d_{11}) & \ldots & \det(d_{1c})\\ \vdots & & \vdots\\ \det(d_{r1}) & \ldots & \det(d_{rc}) \end{pmatrix}.$ ⁷

Menores de una matriz

Además del determinante de una matriz cuadrada, dada una matriz se pueden definir otras magnitudes mediante el empleo de determinantes relacionadas con las propiedades algebraicas de dicha matriz. En concreto dada una matriz cuadrada o rectangular se pueden definir los llamados determinantes menores de orden r a partir del determinante de submatrices cuadradas de rxr de la matriz original. Dada la matriz $\mathbf{A} = [a_{ij}]$ :

$\mathbf{A}= \begin{bmatrix} a_{11} & \dots & a_{1n}\\ \dots & \dots & \dots\\ a_{m1} & \dots & a_{mn} \end{bmatrix}$

Se define cualquier menor de rango r como:

$\begin{vmatrix} a_{i_1j_1} & \dots & a_{i_1j_r}\\ \dots & \dots & \dots\\ a_{i_rj_1} & \dots & a_{i_rj_r} \end{vmatrix}, \qquad \begin{cases} 1\le i_1 < i_2 < \dots < i_r \le n\\ 1\le j_1 < j_2 < \dots < j_r \le m \end{cases}$

Debe notarse que en general existirá un número elevado de menores de orden r, de hecho el número de menores de orden r de una matriz mxnviene dado por:

$\mbox{Min}_r^{m\times n}={m \choose r}{n \choose r}$

Una propiedad interesante es que el rango coincide con el orden del menor no nulo más grande posible, siendo el cálculo de menores una de los medios más empleados para calcular el rango de una matriz o de una aplicación lineal.

Determinante de orden uno

|a₁₁| = a ₁₁

|-2| = -2

Determinante de orden dos

= a ₁₁ a ₂₂ - a ₁₂ a ₂₁

Determinante de orden tres

Se aplica la regla de Sarrus:

positivo negativo

sarrus

Cálculo de un determinante de cualquier orden

Consiste en conseguir que una de las líneas del determinante esté formada por elementos nulos, menos uno: el elemento base o pivote, que valdrá 1 ó -1 .

Seguiremos los siguientes pasos:

1.Si algún elemento del determinante vale la unidad, se elige una de las dos líneas: la fila o la columna, que contienen a dicho elemento (se debe escoger aquella que contenga el mayor número posible de elementos nulos).

Determinante de orden 4

2.En caso negativo:

1. Nos fijamos en una línea que contenga el mayor número posible de elementos nulos y operaremos para que uno de los elementos de esa línea sea un 1 ó -1 (operando con alguna línea paralela ).

Determinante

2.Dividiendo la línea por uno de sus elementos, por lo cual deberíamos multiplicar el determinante por dicho elemento para que su valor no varie. Es decir sacamos factor común en una línea de uno de sus elementos.

Determinante

3.Tomando como referencia el elemento base, operaremos de modo que todos los elementos de la fila o columna, donde se encuentre, sean ceros.

Operaciones

4.Tomamos el adjunto del elemento base, con lo que obtenemos un determinante de orden inferior en una unidad al original.

Adjunto = 2(-58)

matenumerica RUIZ RUEDA LUIS

lunes, 1 de diciembre de 2008

CALCULO DE DETERMINANTES

Determinantes de orden superior a 3

Primeros ejemplos: áreas y volúmenes

Determinante de dos vectores en el plano euclídeo

Propiedades

Generalización [editar]

Determinante de tres vectores en el espacio euclídeo [editar]

Propiedades [editar]

Propiedades

Matrices en bloques [editar]

Menores de una matriz

Determinante de orden uno

Determinante de orden dos

Determinante de orden tres

Cálculo de un determinante de cualquier orden

No hay comentarios:

Seguidores

Archivo del blog

Datos personales