matenumerica RUIZ RUEDA LUIS: 2008

REGLA DEL TRAPECIO

Corresponde al caso donde , es decir :

donde es un polinomio de interpolación (obviamente de grado 1) para los datos:

Del capítulo anterior, sabemos que este polinomio de interpolación es:

Integrando este polinomio, tenemos que:

Por lo tanto, tenemos que:

Que es la conocida Regla del Trapecio. Este nombre se debe a la interpretación geométrica que le podemos dar a la fórmula. El polinomio de interpolación para una tabla que contiene dos datos, es una línea recta. La integral, corresponde al área bajo la línea recta en el intervalo , que es precisamente el área del trapecio que se forma.

Ejemplo 1:
Utilizar la regla del trapecio para aproximar la integral:

Solución.
Usamos la fórmula directamente con los siguientes datos:

Por lo tanto tenemos que:

Ejemplo 2.
Usar la regla del trapecio para aproximar la integral:

Solución.
Igual que en el ejemplo anterior, sustituímos los datos de manera directa en la fórmula del trapecio. En este caso, tenemos los datos:

Por lo tanto, tenemos que:

La regla del trapecio se puede ampliar si subdividimos el intervalo en subintervalos, todos de la misma longitud .

Sea la partición que se forma al hacer dicha subdivisión. Usando propiedades de la integral tenemos que:

Aplicando la regla del trapecio en cada una de las integrales, obtenemos:

Ahora bien, ya que todos los subintervalos tienen la misma longitud h, tenemos que:

Sustituyendo el valor de h y usando la notación sigma, tenemos finalmente:

Esta es la regla del trapecio para n subintervalos. Obviamente, esperamos que entre más subintervalos usemos, mejor sea la aproximación a la integral.

Ejemplo 1:
Aplicar la regla del trapecio para aproximar la integral

si subdividimos en 5 intervalos.

Solución.
En este caso, identificamos , y la partición generada es:

Así, aplicando la fórmula tenemos que:

= 1.48065

Cabe mencionar que el valor verdadero de esta integral es de 1.4626…

Así, vemos que con 5 intervalos, la aproximación no es tan mala. Para hacer cálculos con más subintervalos, es conveniente elaborar un programa que aplique la fórmula con el número de subintervalos que uno desee. El lector debería hacer su propio programa y checar con 50, 500, 1000, 10000 y 20000 subintervalos, para observar el comportamiento de la aproximación.

REGLA DE SIMPSON SIMPLE Y COMPUESTA

La función f(x) (azul) es aproximada por una función cuadrática P(x) (rojo).

En análisis numérico, la regla o método de Simpson (nombrada así en honor de Thomas Simpson) es un método de integración numérica que se utiliza para obtener la aproximación de la integral:

$\int_{a}^{b} f(x) \, dx \approx \frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right]$ .

Derivación de la regla de Simpson

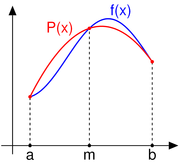
Consideramos el polinomio interpolante de orden dos $P 2 (x)$ , que aproxima a la función integrando $f(x)$ entre los nodos x₀ = a, x₁ = b y m = (a+b)/2. La expresión de ese polinomio interpolante, expresado a través de la Interpolación polinómica de Lagrange es:

$P_2(x)=f(a)\frac{(x-m)(x-b)}{(a-m)(a-b)}+ f(m)\frac{(x-a)(x-b)}{(m-a)(m-b)}+ f(b)\frac{(x-a)(x-m)}{(b-a)(b-m)} .$

Así, la integral buscada se puede aproximar como:

$\int_{a}^{b} f(x) \, dx\approx \int_{a}^{b} P_2(x) \, dx =\frac{h}{3}\left[f(a) + 4f(m)+f(b)\right].$

Error

El error al aproximar la integral mediante la Regla de Simpson es

$-\frac{h^5}{90}f^{(4)}(\xi),$

donde $h = (b - a) / 2$ y $\xi \in [a, b]$ .

Regla de Simpson compuesta

En el caso de que el intervalo [a,b] no sea lo suficientemente pequeño, el error al calcular la integral puede ser muy grande. Para ello, se recurre a la fórmula compuesta del trapecio. Dividiremos el intervalo [a,b] en n subintervalos iguales, de manera que $x i = a + i h$ , donde $h = (b - a) / n$ para $i = 0,1,..., n$ .

Aplicando la Regla de Simpson a cada subintervalo, tenemos:

$\int_{x_{j-1}}^{x_j} f(x)\, dx = \frac{x_{j}-x_{j-1}}{6}\left[f(x_{j-1}) + 4f\left(\frac{x_{j-1}+x_j}{2}\right)+f(x_j)\right] j=1, ..., n.$

Sumando las integrales de todos los subintervalos, llegamos a que:

$\int_a^b f(x) \, dx\approx \frac{h}{3}\bigg[f(x_0)+2\sum_{j=1}^{n/2-1}f(x_{2j})+ 4\sum_{j=1}^{n/2}f(x_{2j-1})+f(x_n) \bigg],$

El máximo error viene dado por la expresión $-\frac{h^4}{180}(b-a)f^{(4)}(\xi).$

METODO DE GAUSS

El Método de Gauss-Seidel Es una técnica utilizada para resolver sistemas de ecuaciones lineales. El método es llamado de esa manera en honor a los matemáticos alemanes Carl Friedrich Gauss y Philipp Ludwig von Seidel. El método es similar al método de Jacobi. Es un método indirecto, lo que significa que se parte de una aproximación inicial y se repite el proceso hasta llegar a una solución con un margen de error tan pequeño como se quiera. Buscamos la solución a un sistema de ecuaciones lineales, en notación matricial:

$A x = b.\,$

El método de iteración Gauss-Seidel es

$x^{(k+1)} = M x^{(k)} + c.\,$

donde

$m_{ij}=0\,$ para i=j, o $\frac {-a_{ij}}{a_{ii}}\,$ para $i\ne j\,$ .

$c_{ij}=\frac {b_{ij}}{a_{ii}}\,$

Esto es también que :

$A = N-P\,$ definimos

$M = N^{-1}P\,$

$c= N^{-1}b\,$ .

Considerando el sistema Ax=b, con la condición de que $a_{ii}{\neq}0 \,$ , i= 1, ..., n. Entonces podemos escribir la fórmula de iteración del método

$x_i^{(k+1)}=\frac{-\sum_{1{\leq}j{\leq}i-1}a_{ij}x_{j}^{(k+1)}-\sum_{i+1{\leq}j{\leq}n}a_{ij}x_{j}^{(k)}+b_i}{a_{ii}} \,$ , i=1,...,n(*)

La diferencia entre este método y el de Jacobi es que, en este último, las mejoras a las aproximaciones no se utilizan hasta completar las iteraciones.

Convergencia

TEOREMA

Suponga una matriz Aε R(n,n) es una matriz no singular cumple la condición de

$\text{[math]}$ \sum_{1{\leq}\nu{\leq}n, \nu{\neq}\mu} |a_{\mu \nu}| \, " src="http://upload.wikimedia.org/math/6/a/f/6afe2026a96bc9abdf5924512ecdfb61.png" style="border-top-style: none; border-right-style: none; border-bottom-style: none; border-left-style: none; border-width: initial; border-color: initial; vertical-align: middle; "> ó $\sum_{1{\leq}\nu{\leq}n, \nu{\neq}\mu} |a_{\nu \mu}|, 1{\leq}\mu{\leq}n \,$ .

Entonces el método de Gauss-Seidel converge a una solución del sistema de ecuaciones Ax=b, y la convergencia es por lo menos tan rápida como la convergencia del método de Jacobi.

Para ver los casos en que converge el método primero mostraremos que se puede escribir de la siguiente forma:

$x^{(k+1)}= B x^{(k)} , k=1,2,3... \,$ (**)

(el término $x^{(k)} \,$ es la aproximación obtenida después de la k-ésima iteración) este modo de escribir la iteración es la forma general de un método iterativo estacionario.

Primeramente debemos demostrar que el problema lineal que queremos resolver se puede representar en la forma (**), para este motivo debemos escribir de escribir la matriz A como la suma de una matriz triangular inferior, una diagonal y una triangular superior A=D(L+I+U),D=diag( $a_{ii} \,$ ). Haciendo los despejes necesarios escribimos el método de esta forma

$x^{(k+1)}{(L+I)}=-{U}x^{(k)}+{D}^{-1}b \,$

por lo tanto B=-(L+I)^(-1) U.

Ahora podemos ver que la relación entre los errores, el cuál se puede calcular al substraer x=Bx+c de (**)

$x^{(k+1)}-x=B(x^{(k)}-x= ... =B^{(k+1)}(x^{(0)}-x). \,$

Supongamos ahora que $\lambda_i \,$ , i= 1, ..., n, son los valores propios que corresponden a los vectores propios $u i$ , i= 1,..., n, los cuales son linealmente independientes, entonces podemos escribir el error inicial

$x^{(0)}-x=\alpha_{1}u_{1}+...+\alpha_{n}u_{n} \,$

$x^{(k)}-x=\alpha_{1}\lambda_{1}^{k}u_{1}+...+\alpha_{n}\lambda_{n}^{k}u_{n} \,$ (***)

Por lo tanto la iteración converge si y sólo si | λi|<1, i=" 1,">

TEOREMA

Una condición suficiente y necesaria para que un método iterativo estacionario $x^{(k+1)}=Bx^{(k)}+c \,$ converge para una aproximación arbitraria x^{(0)} es que

$\rho(B)=max_{1{\leq}i{\leq}n}|\lambda_i|<1 \,$

donde ρ(B) es el radio espectral de B.

Algoritmo

Se elige una aproximación inicial para $x^{0}\,$ .
Se calculan las matrices M y el vector c con las fórmulas mencionadas. El proceso se repite hasta que $x k$ sea lo suficientemente cercano a $x k - 1$ , donde k representa el número de pasos en la iteración.

matenumerica RUIZ RUEDA LUIS

lunes, 15 de diciembre de 2008

lunes, 1 de diciembre de 2008